FractalFun
Benoît Mandelbrot, creator of the Theory of Fractals
A fractal is not a common image, it is a mathematical object with an unconventional third dimension that hides an entire universe perfectly defined by its formula. If you explore that dimension you can navigate between complex structures of incredible beauty where mathematics becomes art, and you will discover corners never seen by anyone, to which you will surely not be able to return if you do not take note of the paths that led you there...
Sergio CT
What is Fractal Geometry?
Fractal Geometry is a relatively modern and little-known branch of mathematics that remained for the most part unstudied due to the large volume of computation it requires. But today, thanks to technological advances...
read more
FractalFun Project
Fractal Geometry is present in great advances in fields of study as different as medicine, biology, astronomy, geography, architecture and technology, among others. It is evident that, in addition to offering extracurricular content to...
read more
Software to explore Fractals
FFExplorer is a software for Windows, portable and free, that has been created according to the philosophy of the "FractalFun Project" for experimentation with fractals in a simple and intuitive way. Since it made the leap to the Internet in 2010...
read more
Fractal art
The concept of art admits many interpretations, which makes its definition very difficult, but it could be said that the most widespread speak of its aesthetic and communicative capacity to transmit ideas and feelings, that is...
learn more
Juliter Transformation
The "Juliter Transformation" arises during the development of new functionalities for FFExplorer and as a test of the hypothesis that fractals can be represented with a...
read more
Orbit trap with Superformula
When I became aware of the existence of the "Superformula" equation, it seemed to me that it was versatile enough to adapt it to an orbit trap generation algorithm that would...
read more
Mirror Plane Transformation
An example of this is the new Mirror Plane Transformation, which owes its name to the fact that, when it is applied to any complex plane fractal, the fractal unfolds into two deformed versions...
read more
About FractalFun
It all started in 2008, I don’t remember the date, I just remember that nothing could calm down my need of be active so I started t oread. I love science, and...
read more
Collaborate
Help FractalFun is quite easy. You can translate tutorials or content, test beta versions of FFExplorer, send suggestions, etc. If you want to collaborate, please contact at
Fractivism
Fractivism is a new artistic movement, proposed by FractalFun, which offers us the opportunity to promote social changes that improve our reality, transforming collective consciousness and creating a more inclusive, sustainable world in perfect harmony with nature.
read more
GALLERY
or the fantastic galleries of FFExplorer users:
DeviantArt: 
DeviantArt: 
Facebook: FFExplorer
Updates within the latest version (v12.6.4 - 04/22/2024)
Rendering
The possibility of rendering "IFS" type fractals is added to the "High Resolution Renderer".
Features
A new "Boid Network Designer" is added to observe emerging phenomena in "Complex Systems".
The option to create "Eden" type aggregates is added to the "Aggregates Designer".
Fractals
A new "IFS" type algorithm is added: Lévy curve tree.
Two new algorithms are added to the "Buddhabrot" family: Buddhabrot homogeneous and Antibuddabrot homogeneous.
The possibility of rotating the fractals of the "Buddhabrot" family is added.
Usability
The behavior of the rotation controls in the "Edit" form is modified to make their use more intuitive.
And many other improvements, which you may not see but you will notice.
In previous versions...
R&D 12.5
The possibility of delimiting the escape perimeter using the shapes integrated in the application or any supershape defined by the user is added.
Features 12.5
The calculation of the fractal dimension using the Minkowski-Bouligand box counting method is added to the "Linear fractals designer".
Usability 12.5
The possibility of set the desired default aspect-ratio for new canvases is added.
Technology 12.5
The Net Core version is increased to 7 for greater stability and speed.
Features 12.4
A snowflake designer inspired by the symmetry of the hexagonal crystalline system of ice crystals is added.
The capability to create frames for holographic pyramids is added to the Riemann Spheres designer.
Usability 12.4
The capability to resize, rotate, and adjust the opacity of multiple orbit traps together is added..
Colouration 12.4
The capability to adjust the angle, height and colour of lighting is added.
Features 12.3
A cellular automaton designer is added with two modes of use: rule-based or Conway's Game of Life.
Fractals 12.3
The "Mirror Transformation" of the compatible algorithms is added, thus increasing their number to the 217 built-in algorithms.
Technology 12.3
The Framework version is increased to 4.8 and Net Core to 6 for greater stability and speed.
Colouring 12.2
A new angular colouring algorithm for orbit traps is added.
Fractals 12.1
Seventeen new IFS algorithms are added.
Usability 12.1
An "elements picker" that makes it easy to find palettes, themes, orbit traps, shapes, supershapes, formulas and superformulas is added.
"Night Mode" is added, which changes the colours of the interface for a better experience in low light environments.
Fractals 12.0
An user's formulas compiler and designer is added along with examples. With this new feature, FFExplorer has gone from being a software for fractal exploration to a software for experimentation with fractals, facilitating greatly the implementation of new ideas that take advantage of all the application features, without the need for compiling new versions of this.
Colouration 11.2
Phase portrait colouring is added as a variant of escape angle colouring.
The option to create custom orbit traps using the Superformula equation is included. More information here.
R&D 11.1
The Juliter Transformation is included, which allows you to create fractals by combining the Mandelbrot and Julia methods. More information here.
Fractals 11.1
Four new IRF algorithms from the Muller and Parhalley families are added.
Performance 11.1
Thread handling is improved, and the parallel computation option is added to increase the calculation speed.
Colouration 11.1
A post-processing filter is added to adjust the gamma correction of final images.
Lighting algorithm support for Lyapunov-type fractals is added.
Fractals 11.0
Four new fractal algorithms of the family Spider are added.
Four new fractal algorithms of the family Manowar are added.
Four new fractal algorithms of the family Lambda are added.
Random versions of the Mandelbox2D algorithms are added.
Colouration 11.0
The lighting algorithm for colouring by escape time is improved.
Features 11.0
Two new circular framing guides are added.
The option to rotate the canvas window is added.
Technology 11.0
The application code is ported to .Net Core and compiled in a separate package.
Fractals 10.4
Eight new fractal algorithms of the family Magnet are added.
Palettes 10.3
Default palettes are replaced by new versions generated from a color theme of the palettes form.
Parameters 10.2
A parameter is added to numerically adjust the zoom level, which in combination with the central coordinates parameter will allow you to locate known areas of the fractals.
Features 10.1
A renderer of up to 256 Mega pixels is added and the "registration system" that gave access to this type of features in beta phase is eliminated.
Performance 10.0
Use of subprocesses to calculate fractals about 16 times faster than the previous version is implemented.
Colouration 10.0
The possibility of illuminating fractals when using escape angle colouration is added.
Fractals 10.0
The new IFS family is added with 18 example fractals and infinite possibilities.
Security warning when you download software
The main web browsers include a download control system that warns you about the risks when you download unknown software or software that was just created. A message like "This file type can harm your computer" does not mean that it is a malware but rather that you may adopt additional precautions. This is meant to prevent a possible attack between the creation of a new malware and its detection by antivirus systems.
It is recommended to download FFExplorer only from its official site, which is verified by several security services.
in figures
Opinion
LUZ PÉREZ-SÁNCHEZ
Professor of psychology in the Department of Developmental and Educational Psychology, Faculty of Education. Complutense University of Madrid - President of Spanish Society for the Giftedness Study - Headmaster of Programa Estrella (special programme for talented and gifted students)
Although math can seem a very specific subject, it is undeniable its transversality in all fields of society, science and art. Thus its incorporation as area of enrichment or extracurricular subject has been a challenge in the educational field in general and specially in the field of the most doted ones.
The idea is not teach math, but to activate the minds in order to comprehend the numeric world through high motivating activities. Fractal geometry and the project FractalFun has been the system thanks to which this challenge has been achieved in big measure.
Working with fractals, students understand the big relation between mathematics, art, rhythm and nature; they work on different scientific matters with high interest and motivation on this field. These are achievements of high educational interest without doubt.
ZLATKO MAJLINGER
Teacher of physics in elementary schools of „Ivan Goran Kovačić“, Vrbovsko, and „Vladimir Gortan“, Rijeka, Croatia
When I was young, I was delighted with books of Peitgen and Richter about Fractal Geometry. Several decades later, when I was looking for a collaborator for a school project, I found the page FractalFun and immediately got in touch with Sergio. As the amazing result of our cooperation, one-year project of an estimate of Spanish coastline fractal dimension appeared.
I am fully surprised with the level of knowledge and great talent of students involved in FractalFun projects, and I think that Sergio does a great and quality job in a field of education of young talented people. I hope that this our small contribution of Croatian pupils with participation in FractalFun projects will not be the last.
I strongly support Fractivism. Application of Fractal Geometry in art and graphical design is not a new movement, but Sergio gives his own personal touch in this topic. He works wonders in the field of artwork with his own software. FFExplorer is the best computer program for creation of fractal structure I have ever seen, it is rich in original options and unique. I will recommend it to everyone with a wish to explore this beautiful world of Fractal Geometry.
PILAR MUÑOZ DELEITO
Programa ADA (High Learning development) Co-director and coordinator in the Intelligence and Talent Advisory unit of the UCJC
Fractal Geometry is very attractive, motivating element for high academic efficiency students or high motivated students for scientific and artistic learning, as it is a quite modern theory which boom is answering questions never resolved by science before.
ICT has become a great tool in order to understand fractals, which makes the most of its artistic capacity but, is this science or art? It is nature interpreted under math and technology.
The project Fracfinder is a big ally in the vocational professional development; it activates the math, artistic, sociologic thinking, in short, a great tool to enrichen and develop the talent.
FELIPE TORREJÓN SANJUÁN
Head of studies in Primary Education - Colegio Arcadia
Our educative model is based on the learning through skills, understanding that comprehension and learning acquisition are achieved through the content contextualization and transversality. Here is how Fractal Geometry allows to work from both fields, it relates multiple academic areas (math, science, art, ICT) and it allows to comprehend the content functionality learned at the same time by relating directly math’s concepts and procedures with natural processes.
Our year six students (Primary Education) had the great opportunity to enjoy a Fractal Geometry workshop where math blended with nature in a perfect symbiosis. We achieved to work the concept of geometry from a skill-based point of view, but above all we incited our students’ curiosity. There is no doubt of projects like FractalFun’s success in the educational field.
ROYAL SPANISH MATHEMATICAL SOCIETY
The Royal Spanish Mathematical Society (RSME) is a scientific society whose purpose is the promotion and dissemination of Mathematics and its applications, and the encouragement of its research and teaching at all educational levels.
The Royal Spanish Mathematical Society includes a link to the FractalFun Project in the news section "On the Net" of its bulletin number 789, dated January 27, 2023.
#ApuntasTech
The aim of this contest is to «create a catalogue of certain proposals that would help to awake the enthusiasm for technology and help to bring up the early technological vocations in early stages between girls and boys aged 10 to 15»
FractalFun was awarded for its software FFExplorer in the 1st edition of the contest #ApuntasTech, brought by Centro de Supercomputación de Galicia, the Secretaría Xeral da Igualdade de la Xunta, the Colexio Oficial de Enxeñaría Informática and the Asociación de Mujeres Investigadoras y Tecnólogas.
SANTI GARCÍA CREMADES
Mathematician, professor at Miguel Hernandez University of Elche and scientific disseminator in radio and tv programmes
Fractal geometry gets us back to the first concept of mathematics in history: a literacy science, an art full of philosophy, a beautiful and pure artwork.
Working with maths is working in something pure and that a lot. Working in fractal art is something poetic, a bridge between divine and earthly, the infinite observed with our finite eyes, the chaos seen from the biggest possible order.
FractalFun does this, something pure and poetic, what's more, from a unique technology. I can't say anymore, we are finite after all...
Research work
Extract from the conclusions of the research work carried out by two students belonging to the Batxillerat Científic de l'Institut Joan Brossa (Barcelona)
This work has radically changed the way we perceive the real world, since after knowing fractals it is difficult not to appreciate them everywhere.
To define their characteristics we learned to use FFExplorer, a tool that has allowed us to see how they are formed, which has represented a very important part of the work.
At the end, those irregular figures that we thought we would never understand turned out to be extremely simple. We observe that they have many applications, and that most people are not aware of their importance.
We have learned a multitude of things that will certainly help us in our future.
Practical work
Extract from a practical work carried out by a student at the „Vladimir Gortan“ school in Rijeka (Croatia)
The objective of the project is to demonstrate that it is possible to print objects inside others without having to add support material to the interior.
The goal was achieved, and with this pyramid I demonstrated that printing conical shapes upside down within the original shape, instead of other possible shapes, is very profitable.
Why a fractal pyramid?
I chose to make the Sierpinski pyramid because my professor Majlinger introduced the FractalFun project. That Spanish project inspired me to start researching fractals... read more
What is Fractal Geometry?
Fractal Geometry is a relatively modern and little-known branch of mathematics that remained for the most part unstudied due to the large volume of computation it requires. But today, thanks to technological advances, it has been possible to automate and greatly streamline these calculations through the use of computer algorithms, , with which new and unexplored territories are opened up to experiment.
From a mathematical point of view, we talk about the best tool we have to date to understand the natural designs that occur in our environment. But, in addition, Fractal Geometry also allows us to create the impressive works of digital art that we commonly know as Fractals. A fractal is nothing more than the graphical representation of the behavior of a mathematical function, but it is precisely the characteristics of these graphs, so like the characteristics of natural designs, that make Fractal Geometry the « language of nature ».
If you work in a school you may be interested in the “FractalFun Project”
Or maybe you're just looking for a fantastic "Fractal Explorer Software”.
FractalFun Project
Fractal Geometry is present in great advances in fields of study as different as medicine, biology, astronomy, geography, architecture and technology, among others. It is evident that, in addition to offering extracurricular content to our students, Fractal Geometry allows to establish didactic connections between very different areas of study (computer science, mathematics, art, natural sciences, etc.), thus providing an ideal transversality scenario for our students to feel the freedom to take the path they want during their learning process. To this is added the advantage that, whatever direction they take, they will carry with them a good mathematical base that, surely, will be useful in any other area to which they dedicate their time in the future.
With this premise, the FractalFun Project* was born, designed to make known in a simple and intuitive way the concept of "Fractal Geometry" through the use of its own software, FFExplorer, which is constantly evolving since 2010 to facilitate the study and experimentation with fractals.
Currently, different educational enrichment programs are based on the experience of FractalFun with the aim of developing in its students new skills and knowledge that allow them to recognize and apply geometric ideas beyond mathematics itself, such as in art, nature or architecture. In this way, your students are more effective in finding creative solutions to face the problems that arise in their day to day.
As a second objective, but no less important, this project focuses on students developing knowledge that gives them superior skills to those they can resort to tomorrow to face possible situations and problems that arise within their different areas of study or work.
The following videos show some of the activities carried out by the students of the Fractal Geometry Area:
What is a fractal?
Planetary System of Shaula:The Riemann sphere
Research work:Cardioids, epicycles, and diagrams
Fractal Dimension - Collaboration between Croatia and Spain -For more information about the project, please go to
Or maybe you already have a plan and just need a "Fractal Explorer Software"
(*) This project and its software were called "Fractfinder" and "Explorador FF" until 2018.
Software to explore Fractals
FFExplorer is a software for Windows, portable and free, that has been created according to the philosophy of the "FractalFun Project" for experimentation with fractals in a simple and intuitive way. Since it made the leap to the Internet in 2010 it has not stopped evolving, adapting with new algorithms and functionalities to the specific needs of students and institutions that make use of it.
What can you expect from FFExplorer?
If you are going to explore fractals for the first time, the software will offer you the possibility to forget about numbers and formulas. You can fully dedicate yourself to discover and enjoy just by interacting by using the mouse directly on fractal images.
If, on the other hand, this is not your first contact with fractals, the software will offer you the possibility of giving it a more advanced use. You can modify the parameters and behaviors of the algorithms to create countless variations of the original fractals, as well as create your own fractal algorithms from scratch.
FExplorer includes a wide variety of fractal, coloring and lighting algorithms; But you can also find in it a multitude of tools that in one way or another relate to fractals, or interact with them:
- Compiler of formulas for the creation of new algorithms.
- Stereographic projector of fractals on Riemann spheres.
- Generator of fractals by Diffusion Limited Aggregates.
- Generator of kaleidoscopic patterns from fractals.
- Julia map generator from Mandelbrot fractals.
- Cellular noise generator based on Voronoi diagrams.
- Designer of complex orbital traps based on "Superformula".
- Multiplication diagram designer.
- Designer of fractal Pythagoras trees.
- Designer of fractal snowflakes.
- Fractal designer by Sierpiński.
- Designer of Linear fractals.
- Branching diagrams.
- Cellular automatons based on rules or Conway's Game of Life.
- Complex systems based on Craig Reynolds' Boids Model.
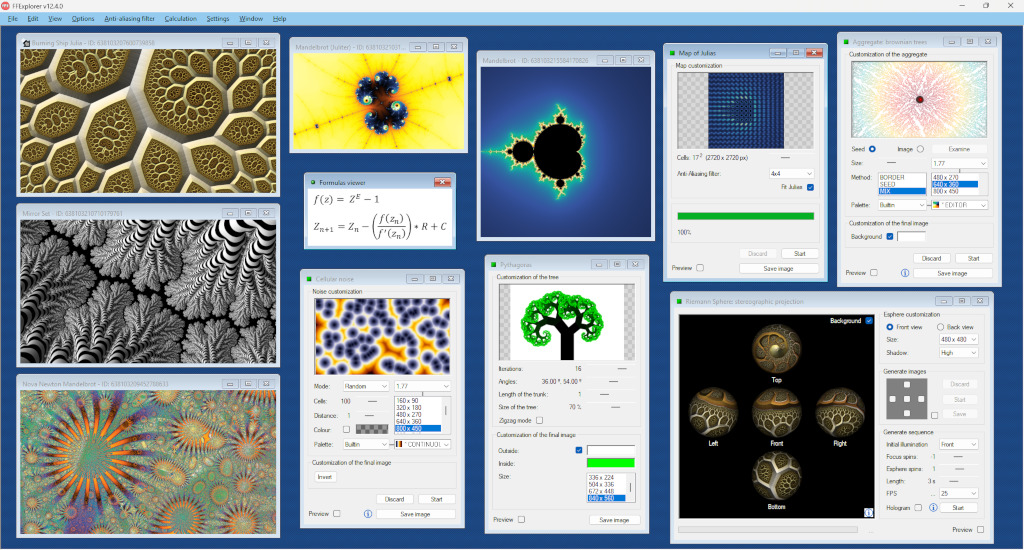
As many of the tools of the software interact with each other, this has been designed with an interface that works as a desktop, to be able to place them freely where you want and thus be able to work with them comfortably.
« FFExplorer is easy to use, versatile and adaptable. With it you get very varied fractal images that can be used for various purposes, including designing amazing animations, or creating Fractal Art of excellent quality. Once the image is generated you can choose to use a graphic editor with which to retouch it, but I personally prefer to look for the desired final aspect for the image just by exploring the fractal, and use it directly without retouching, so that it preserves and shows all its mathematical essence intact. However, in addition to being a software that allows you a great level of control to generate beautiful images with the look you want, FFExplorer does not stop living up to its name, as it allows you to explore fractals, and that is an amazing experience. When I start I can't stop... »
ElenSegu, expert in design and Fractal Art
Here you can download the latest version of "FFExplorer"
And here you can take a look at "FFExplorer in figures"
Fractal art
The concept of art admits many interpretations, which makes its definition very difficult, but it could be said that the most widespread speak of its aesthetic and communicative capacity to transmit ideas and feelings, that is, everything linked to our most emotional part...
So it seems a contradiction when talking about creating art with mathematics, a subject that reminds us of words like "precision", "calculus", "analysis"... cold concepts associated with rational thought and apparently of a nature incompatible with art.
However, all this changed thanks to Fractal Geometry: a fractal is the graphic representation of the behavior of a mathematical formula, with which its author has experimented to achieve the desired appearance. This experimentation consists of the numerical adjustment of certain parameters, the introduction of small transformations and a good treatment of color. With all this, an explorable graphic environment is achieved, in which in addition to the two dimensions of the plane there is a third dimension (unconventional) that is only accessible by zooming. In this virtual world, its creator can move freely and look for the desired area and framing to finish his work.
Fractal art has very exclusive properties:
Complexity. The complex operation of the formulas, apparently simple, is responsible for the great explosion of shapes and colors that give fractal images a great level of detail perceptible at different scales. This makes a piece of art with big proportions show very different details depending on the distance from where it is been watched, being more noticeable its self-similarity feature and the third dimension effect.
Perfection. The appearance of a fractal image is perfectly defined by the configuration of the algorithm that draws it, this means that the formula and the numerical values entered in it are a unique and exclusive hallmark of the image. Knowing this data allows you to redraw it as many times as you want, for example, to continue working on it, or to generate a copy of the original at a higher resolution without loss of quality (but on the contrary, a larger size increases its definition).
Exclusivity. The formula that draws a fractal is very sensitive to the values of its parameters, so that a slight variation in any of them will produce a completely different image. Thanks to this, it is practically impossible to redraw a fractal image if the formula and the exact values that were originally used are not known, which allows to demonstrate who is the author of the image since it prevents someone different from making exact copies of the work.
If you found it interesting, you may want to know what "Fractivism" isOr you can visit the FractalFun Social Networks: