FractalFun
Benoît Mandelbrot, creador de la Teoría de Fractales
Un fractal no es una imagen común, se trata de un objeto matemático con una tercera dimensión no convencional que esconde todo un universo perfectamente definido por su fórmula. Si exploras esa dimensión podrás navegar entre complejas estructuras de increíble belleza donde las matemáticas se convierten en arte, y descubrirás rincones nunca vistos por nadie.
Sergio CT¿Qué es la Geometría Fractal?
La Geometría Fractal es una es una rama de las matemáticas relativamente moderna y poco conocida que permaneció en su mayor parte sin ser estudiada debido al gran volumen de cálculo que requiere. Pero hoy en día, gracias a los avances tecnológicos...
seguir leyendo
Proyecto FractalFun
La Geometría Fractal está presente en grandes avances de campos de estudio tan diferentes como la medicina, biología, astronomía, geografía, arquitectura y tecnología, entre otros. Es evidente que, además de ofrecer contenidos extracurriculares...
seguir leyendo
Software explorador de Fractales
FFExplorer es un software para Windows, portable y gratuito, que ha sido creado de acuerdo con la filosofía del “Proyecto FractalFun” para la experimentación con fractales de forma sencilla e intuitiva. Desde que dio el salto a Internet en 2010...
seguir leyendo
Arte Fractal
El concepto de arte admite muchas interpretaciones, lo que hace muy difícil su definición, pero se podría decir que las más extendidas hablan de su capacidad estética y comunicativa para transmitir ideas y sentimientos, es decir...
seguir leyendo
Transformación Juliter
La "Transformación Juliter" surge durante el desarrollo de nuevas funcionalidades para FFExplorer y como comprobación de la hipótesis de que se pueden representar fractales con una...
seguir leyendo
Trampa orbital con Superfórmula
Cuando tuve conocimiento de la existencia de la ecuación de "Superfórmula", me pareció que esta era suficientemente versátil como para adaptarla en un algoritmo de generación de trampas orbitales que...
seguir leyendo
Transformación de Plano Mirror
Un ejemplo de ello es la nueva Transformación de Plano Mirror, que debe su nombre a que, cuando esta se aplica a cualquier fractal de plano complejo, el fractal se desdobla en dos versiones...
seguir leyendo
Dimensión Fractal
En cambio, el concepto de dimensión fractal es completamente diferente. En este caso, hablamos de un número real que nos ofrece información acerca de la complejidad de un objeto, y de cómo esta...
seguir leyendo
Sistemas caóticos nuevo
¿Se puede predecir el futuro? Desde las predicciones meteorológicas hasta los modelos de ecosistemas, la idea de que el destino esté escrito ha fascinado a filósofos y científicos...seguir leyendo
Trazado de órbitas nuevo
Esta aplicación te permite iterar la Función de Mandelbrot utilizando como valor de C las coordenadas del punto que selecciones en el plano...ir a la aplicación web
Algoritmo de Paleta Extendida nuevo
Este documento describe un método para ampliar dinámicamente una paleta de colores de forma que se elimine la repetición perceptible de patrones cromáticos típica de los fractales generados mediante algoritmos de tiempo de escape...seguir leyendo
Fractivismo
El Fractivismo es un nuevo movimiento artístico, propuesto por FractalFun, que nos ofrece la oportunidad de impulsar cambios sociales que mejoren nuestra realidad, transformando la conciencia colectiva y creando un mundo más inclusivo, sostenible y en perfecta armonía con la naturaleza.
seguir leyendo
Acerca de FractalFun
Todo comenzó en 2008, no ocurría nada que calmase mi necesidad de estar siempre activo, así que me puse a leer. Me encanta la ciencia, y aquel día...
seguir leyendo
Colaborar
Ayudar a FractalFun es muy fácil. Puedes traducir tutoriales o contenido, probar versiones beta de FFExplorer, enviar sugerencias, etc. Si deseas colaborar, por favor dirígete a

GALERÍA
o las fantásticas galerías de los usuarios de FFExplorer:
FFExplorer
Novedades en la última versión (v13.2.1 - 21/01/2026)
Coloración
Se añade un nuevo algoritmo para extender la paleta de color eliminando la percepción de patrones cromáticos repetitivos.
Usabilidad
Se añade un previsualizador de zoom para buscar puntos interesantes durante la exploración.
Rendimiento
Se refactorizan varias partes clave del código para un mayor rendimiento y estabilidad de la aplicación.
Y muchas mejoras más, que no se ven pero se notan.
En versiones anteriores...
Funcionalidades 13.1
Se implementan dos nuevos algoritmos para generar atractores extraños: Lorenz y Simone.
Se añade un filtro antialias para diagramas de bifurcación.
Se añade al formulario de parámetros la posibilidad de generar valores aleatorios.
Rendimiento 13.1
Se optimizan los algoritmos para diagramas de bifurcación, buddhabrot, sistemas de funciones iteradas (IFS) y descriptores lagrangianos discretos (DLD).
Coloración 13.1
Se añade un nuevo tipo de coloración para diagramas de bifurcación basado en tono, saturación y luminosidad (HSL).
Usabilidad 13.1
Se personalizan los títulos de los cuadros de diálogo para que sean más representativos.
Se sustituyen algunos iconos de los menús para que sean más representativos.
I+D 13.0
Se añade un renderizador de "Descriptores Lagrangianos Discretos" (DLD).
Se añade un diseñador de laberintos basado en el algoritmo "Depth First Search" (DFS).
Coloración 13.0
Se añade la forma de escape "Cardioide" al algoritmo de tiempo de escape.
Usabilidad 13.0
Se añade la opción de guardar imágenes desde el menú "archivo" para herramientas que tienen su propio menú o botón de guardar imagen.
Coloración 12.7
Se hace una mejor gestión del canal Alpha para mejorar las trampas orbitales semitransparentes.
Rendimiento 12.7
Se optimizan los algoritmos de iluminación y de suavizado para reducir el tiempo de cálculo.
Se mejora la velocidad de los algoritmos de trampa orbital con forma de cardioide.
Se realizan varias optimizaciones para aumentar el rendimiento en equipos con hardware antiguo.
Usabilidad 12.7
Se hace más intuitivo el uso de la Transformación Juliter y de la Trampa Orbital Múltiple.
Se añaden nuevos menús para el acceso directo a diferentes funcionalidades de edición.
Se añade la posibilidad de importar paquetes de patrones de trampa orbital.
Se añaden tamaños de imagen con orientación vertical para dispositivos móviles.
Se añade el soporte de archivos WebP y SVP para trampa orbital.
Se actualizan los mapas de bits en tiempo de ejecución cuando son reemplazados por otro archivo.
Tecnología 12.7
Se aumenta la versión de Net Core a la 8 para lograr mayor estabilidad y velocidad.
Se refactoriza código con el objetivo de hacer la aplicación más robusta y escalable.
Se añade compatibilidad con pantallas configuradas con escalado de imagen.
Renderizado 12.6
Se añade al "Renderizador de Alta Resolución" la posibilidad de renderizar fractales de tipo "IFS".
Funcionalidades 12.6
Se añade un nuevo "Diseñador de Redes de Boids" para observar fenómenos emergentes en "Sistemas Complejos".
Se añade al "Diseñador de agregados" la opción de crear agregados de tipo "Edén".
Se añade al "Diseñador de Autómatas celulares" dos nuevos algoritmos "Multiestado", basados en el juego de "Piedra, Papel o Tijera".
Fractales 12.6
Se añade un nuevo algoritmo de tipo "IFS": Árbol curva de Lévy.
Se añaden dos nuevos dos algoritmos a la familia "Buddhabrot": Buddhabrot homogéneo y AntiBuddabrot homogéneo.
Se añade la posibilidad de rotar los fractales de la familia "Buddhabrot".
Usabilidad 12.6
Se modifica el comportamiento de los controles de rotación, del formulario de "Edición" para que su uso sea más intuitivo.
I+D 12.5
Se añade la posibilidad de delimitar el perímetro de escape utilizando las formas integradas en la aplicación o cualquier superforma definida por el usuario.
Funcionalidades 12.5
Se añade al "Diseñador de Fractales lineales" el cálculo de la dimensión fractal mediante el método de conteo de cajas de Minkowski-Bouligand.
Usabilidad 12.5
Se añade la posibilidad de configurar la relación de aspecto por defecto deseada para los nuevos lienzos.
Tecnología 12.5
Se aumenta la versión de Net Core a la 7 para lograr mayor estabilidad y velocidad.
Funcionalidades 12.4
Se añade un diseñador de copos de nieve inspirado en la simetría del sistema cristalino hexagonal de los cristales de hielo.
Se añade al diseñador de Esferas de Riemann la posibilidad de crear fotogramas para pirámides holográficas.
Usabilidad 12.4
Se añade la posibilidad de redimensionar, rotar y ajustar la opacidad de trampas orbitales múltiples en conjunto.
Coloración 12.4
Se añade la posibilidad de ajustar el ángulo, la altura y el color de la iluminación.
Funcionalidades 12.3
Se añade un diseñador de autómatas celulares con dos modos de uso: basado en reglas o en el Juego de la Vida de Conway.
Fractales 12.3
Se añade la "Transformación Mirror" de los algoritmos compatibles, con lo que aumenta su número hasta los 217 algoritmos integrados.
Tecnología 12.3
Se aumenta la versión de Framework a la 4.8 y de Net Core a la 6 para lograr mayor estabilidad y velocidad.
Coloración 12.2
Se añade un nuevo algoritmo de coloración angular para trampa orbital.
Fractales 12.1
Se añaden diecisiete nuevos algoritmos IFS.
Usabilidad 12.1
Se añade un "selector de elementos" que facilita la búsqueda de paletas, temas, trampas orbitales, formas, superformas, fórmulas y superfórmulas.
Se añade el "Modo noche", que cambia los colores de la interfaz para una mejor experiencia en entornos con poca luz.
Fractales 12.0
Se añade un diseñador y compilador de fórmulas de usuario acompañado de ejemplos. Con esta nueva característica, FFExplorer ha pasado de ser un software para la exploración de fractales a ser un software para la experimentación con fractales, facilitando enormemente la implementación de nuevas ideas que aprovechan todas las características de la aplicación, sin necesidad de compilar nuevas versiones de esta.
Coloración 11.2
Se añade la coloración por retrato de fase como variante de la coloración por ángulo de escape.
Se incluye la posibilidad de crear trampas orbitales personalizadas mediante la ecuación de Superfórmula. Más información aquí.
I+D 11.1
Se incluye la Transformación Juliter, que permite crear fractales combinando los métodos de Mandelbrot y de Julia. Más información aquí.
Fractales 11.1
Se añaden cuatro nuevos algoritmos IRF de las familias Muller y Parhalley.
Rendimiento 11.1
Se mejora la gestión de subprocesos y se añade la opción de cálculo en paralelo para aumentar la velocidad de cálculo.
Coloración 11.1
Se añade un filtro de post-procesado para ajustar la corrección gamma de imágenes finales.
Se añade la compatibilidad del algoritmo de iluminación con fractales de tipo Lyapunov.
Fractales 11.0
Se añaden cuatro nuevos algoritmos fractales de la familia Spider.
Se añaden cuatro nuevos algoritmos fractales de la familia Manowar.
Se añaden cuatro nuevos algoritmos fractales de la familia Lambda.
Se añaden versiones aleatorias de los algoritmos Mandelbox2D.
Coloración 11.0
Se mejora el algoritmo de iluminación para coloración por tiempo de escape.
Funcionalidades 11.0
Se añaden dos nuevas guías de encuadre circulares.
Se añade la posibilidad de rotar la ventana del lienzo.
Tecnología 11.0
Se hace la portabilidad del código de la aplicación a .Net Core y se compila en un paquete aparte.
Fractales 10.4
Se añaden ocho nuevos algoritmos fractales de la familia Magnet.
Paletas 10.3
Se sustituyen las paletas de color por defecto por nuevas versiones generadas a partir de un trema de color del formulario de paletas.
Parámetros 10.2
Se añade un parámetro para ajustar numéricamente el nivel de zoom, que en combinación con el parámetro de coordenadas centrales permitirá localizar zonas conocidas de los fractales.
Funcionalidades 10.1
Se añade un renderizador de hasta 256 Mega pixeles y se elimina el "sistema de registro" que daba acceso a este tipo de características en fase beta.
Rendimiento 10.0
Se implementa el uso de subprocesos para calcular fractales unas dieciséis veces más rápido que en la versión anterior.
Coloración 10.0
Se añade la posibilidad de iluminar fractales que utilizan coloración basada en ángulo de escape.
Fractales 10.0
Se añade la nueva familia IFS, con 18 fractales de ejemplo e infinidad de posibilidades.
Advertencias de seguridad al descargar software
Los principales navegadores de Internet incluyen un sistema de control de descargas que advierte del riesgo que supone descargar software poco conocido o de muy reciente creación. Un mensaje como "Este tipo de archivo puede dañar tu ordenador" no quiere decir que el software sea malicioso, sino que debes tomar precauciones adicionales. Con ello se pretende reducir los ataques entre la aparición de un nuevo malware y su detección por los sistemas antivirus.
Se recomienda descargar FFExplorer sólo desde su sitio web oficial, que está verificado por diferentes servicios de seguridad.
Descargas
Más descargas
Más tutoriales

en cifras

Opinión
REAL SOCIEDAD MATEMÁTICA ESPAÑOLA
La Real Sociedad Matemática Española es una sociedad científica cuyo fin es la promoción y divulgación de las Matemáticas y sus aplicaciones, y el fomento de su investigación y enseñanza en todos los niveles educativos.
La Real Sociedad Matemática Española incluye en la sección de noticias “En la Red”, de su boletín número 789, del 27 de enero de 2023, un enlace al Proyecto FractalFun.
ZLATKO MAJLINGER
Profesor de física en las escuelas de primaria „Ivan Goran Kovačić“, Vrbovsko, y „Vladimir Gortan“, Rijeka, Croacia
Cuando era joven, me encantaban los libros de Peitgen y Richter sobre Geometría Fractal. Varias décadas después, cuando buscaba un colaborador para un proyecto escolar, encontré la página de FractalFun e inmediatamente me puse en contacto con Sergio. Como resultado sorprendente de nuestra cooperación, hicimos un proyecto de un año de duración para el cálculo de la dimensión fractal de la costa española. Seguir leyendo
Estoy completamente sorprendido con el nivel de conocimiento y el gran talento de los estudiantes involucrados en los proyectos de FractalFun, y creo que Sergio hace un trabajo excelente y de calidad en el campo de la educación de jóvenes talentos. Espero que nuestra pequeña contribución, con alumnos croatas participando en proyectos de FractalFun, no sea la última.
Apoyo firmemente el Fractivismo. El uso de la Geometría Fractal en el arte y en el diseño gráfico no es un movimiento nuevo, pero Sergio le da su toque personal a este tema. Hace maravillas en el campo del arte con su propio software. FFExplorer es el mejor programa informático para la creación de estructuras fractales que he visto, es rico en opciones originales y únicas. Se lo recomendaré a todos los que deseen explorar este hermoso mundo de la Geometría Fractal.
Cálculo de la dimensión fractal de la costa española#ApuntasTech
El objetivo de este certamen es «crear un catálogo de propuestas concretas que ayuden a despertar el entusiasmo por la tecnología y alienten las vocaciones tecnológicas tempranas entre niñas y niños de 10 a 15 años».
FractalFun premiado por su software FFExplorer en la primera edición del concurso #ApuntasTech, convocado por el Centro de Supercomputación de Galicia, la Secretaría Xeral da Igualdade de la Xunta, el Colexio Oficial de Enxeñaría Informática y la Asociación de Mujeres Investigadoras y Tecnólogas.
LUZ PÉREZ-SÁNCHEZ
Catedrática de Psicología Evolutiva y de la Educación - Presidenta de la Sociedad Española para el Estudio de la Superdotación - Directora del Programa Estrella para alumnos con Alta Capacidad y Talento
Aunque las matemáticas puedan parecer una materia muy específica es innegable su transversalidad en todos los campos de la sociedad, de la ciencia y del arte. De ahí que su incorporación como área de enriquecimiento o actividad extraescolar haya sido un reto en el campo educativo en general y especialmente en el de los alumnos más dotados. Seguir leyendo
La idea no es enseñar matemáticas, sino activar la mente para comprender el mundo numérico a través de actividades realmente motivadoras. La Geometría Fractal y el Proyecto FractalFun han sido en una gran medida el sistema que ha permitido cumplir este reto.
Trabajando con fractales, los alumnos entienden la gran relación existente entre las matemáticas, el arte, el ritmo y la naturaleza; realizan trabajos científicos de gran interés y con una gran motivación hacia este campo. Estos son sin duda logros de máximo interés pedagógico.
FELIPE TORREJÓN SANJUÁN
Jefe de estudios de Educación Primaria - Colegio Arcadia
Nuestro modelo educativo se basa en el aprendizaje por competencias, entendiendo que la comprensión y el anclaje del aprendizaje se consiguen mediante la contextualización y transversalidad del contenido. En esta línea la Geometría Fractal permite trabajar desde ambos ámbitos, supone la relación entre varias áreas académicas (matemáticas, ciencias, arte e informática), y a la vez permite comprender la funcionalidad del contenido que se aprende, al relacionar directamente conceptos y procedimientos matemáticos con procesos naturales. Seguir leyendo
Nuestros alumnos de sexto de educación primaria tuvieron la oportunidad de disfrutar de un taller de Geometría Fractal en el que las matemáticas se fundieron con la naturaleza en una simbiosis perfecta. Conseguimos trabajar la geometría desde un punto de vista competencial, pero sobre todo logramos provocar curiosidad en el alumnado. No cabe la menor duda del éxito de proyectos como FractalFun en el ámbito educativo.
SANTI GARCÍA CREMADES
Matemático, profesor de la Universidad Miguel Hernández de Elche y divulgador científico en programas de radio y televisión
La Geometría Fractal nos hace volver al primer concepto de las Matemáticas en la historia: una ciencia de letras, un arte lleno de filosofía, una obra bella y pura. Seguir leyendo
Trabajar las Matemáticas es trabajar en algo puro, y eso ya es mucho decir. Trabajar en el arte fractal es algo poético, un puente entre lo terrenal y lo divino, el infinito observado con nuestros ojos finitos, el caos observado desde el mayor orden posible.
FractalFun hace esto, algo puro y poético, y además, desde una tecnología única. No os digo más, que somos finitos...
Trabajo de investigación
Extracto de las conclusiones del trabajo de investigación realizado por dos alumnos pertenecientes al Batxillerat Científic de l'Institut Joan Brossa (Barcelona)
Este trabajo nos ha cambiado radicalmente la forma en la que percibimos el mundo real, ya que después de conocer los fractales resulta difícil no apreciarlos en todas partes. Seguir leyendo
Para definir sus características aprendimos a utilizar FFExplorer, una herramienta que nos ha permitido ver cómo se forman, lo que ha representado una parte muy importante del trabajo.
Al finalizar, aquellas figuras irregulares que pensábamos que nunca llegaríamos a entender, resultaron extremadamente simples. Observamos que tienen muchas aplicaciones, y que la mayoría de las personas no son conscientes de su importancia.
Hemos aprendido una multitud de cosas que con total certeza nos servirán para nuestro futuro.
PILAR MUÑOZ DELEITO
Co-directora y coordinadora del Programa ADA (Alto Desarrollo del Aprendizaje) de la Unidad de Asesoramiento en Inteligencia y Talento de la UCJC
La Geometría Fractal ejerce un gran atractivo, es un elemento muy motivador para los estudiantes de alto rendimiento académico o con alta motivación por el aprendizaje, tanto científico como artístico, ya que al ser una teoría bastante moderna se encuentra en pleno auge, dando respuestas a cuestiones para las que la ciencia aún no las tenía. Seguir leyendo
La informática se ha convertido en la gran herramienta para comprender los Fractales, con la que además se puede sacar provecho de su capacidad artística ¿Pero esto es ciencia o es arte? se trata de la naturaleza misma interpretada a través de las matemáticas y de la tecnología...
El Proyecto FractalFun es un gran aliado en el desarrollo de vocaciones profesionales; activa el pensamiento matemático, artístico, sociológico, en definitiva una gran herramienta para el enriquecimiento y desarrollo del talento.
GREGORIO LLANA SUÁREZ
Departamento de Matemáticas del Instituto Español Juan Ramón Jiménez, Casablanca (Marruecos)
Cada año, la Red de Centros Docentes Españoles en Marruecos organiza las Olimpiadas Matemáticas para su alumnado de secundaria. Son dos jornadas de convivencia que incluyen visitas culturales, conferencias, talleres, concurso de fotografía y las competiciones individuales y por equipos. En 2025, nuestro centro acogió la XXVIII edición, y propusimos a Sergio que ofreciera una conferencia introductoria sobre los fractales, seguida de un taller práctico para explorar estos conceptos. Queríamos que fuera una experiencia más manipulativa y motivadora, no solo teórica. Seguir leyendo
El taller se ofreció tanto al alumnado del centro como a los participantes de la Olimpiada, y el resultado fue excepcional. Los estudiantes entendieron bien qué es un fractal y cómo se genera, y pusieron en práctica estas ideas con el software FFExplorer. A muchos les sorprendió la recurrencia de las formas y el uso del color, y varios comentaron que el taller se les hizo corto, pero que pensaban seguir trabajando en ello desde casa, lo que demuestra el verdadero interés que despertó la actividad. Una de las grandes virtudes fue que todo el alumnado, independientemente de su nivel en matemáticas, se implicó y obtuvo resultados con los que quedaron satisfechos.
A título personal, me sorprendieron especialmente dos cosas: cómo de unas condiciones iniciales simples surgen estructuras de gran complejidad, y el papel del color en la percepción de las formas. Normalmente estudiamos las gráficas de funciones en blanco y negro, pero al introducir el color, la percepción cambia por completo.
Elegir la Geometría Fractal como tema de estas Olimpiadas resultó ser todo un acierto, tanto por el interés que despertó como por la implicación que logró en el alumnado. Iniciativas como el Proyecto FractalFun tienen un gran valor educativo, ya que acercan a los estudiantes a conceptos matemáticos que estimulan su curiosidad, creatividad y ganas de seguir aprendiendo.
XXVIII Olimpiada Matemática (Marruecos)Trabajo práctico
Extracto de un trabajo práctico realizado por un alumno de la escuela „Vladimir Gortan“ de Rijeka (Croacia)
El objetivo del proyecto es demostrar que es posible imprimir objetos dentro de otros sin necesidad de añadir material de soporte al interior. Seguir leyendo
El objetivo se logró, y con esta pirámide demostré que imprimir formas cónicas al revés dentro de la forma original, en lugar de otras formas posibles, es muy rentable.
¿Por qué una pirámide fractal?
Elegí hacer la pirámide de Sierpinski porque mi profesor Majlinger me presentó el proyecto FractalFun. Ese proyecto español me inspiró a empezar a investigar los fractales.
¿Qué es la Geometría Fractal?
La Geometría Fractal es una es una rama de las matemáticas relativamente moderna y poco conocida, que permaneció mucho tiempo sin ser estudiada debido al gran volumen de cálculo que requería. Hoy en día, mediante el uso de algoritmos informáticos se han podido automatizar y agilizar dichos cálculos, abriéndose así nuevos e inexplorados territorios donde experimentar.
Desde un punto de vista matemático, hablamos de la mejor herramienta que tenemos para comprender los diseños que se producen de forma natural en nuestro entorno. Pero, además, la Geometría Fractal también nos permite crear las complejas obras de arte digital que comúnmente conocemos como Fractales. Son precisamente las características de estos gráficos, tan similares a las características de los diseños naturales, las que convierten a la Geometría Fractal en el « lenguaje de la naturaleza ».

Si trabajas en un colegio quizás te interese el “Proyecto FractalFun”
O puede que sólo estés buscando un fantástico "Software explorador de Fractales”.
Proyecto FractalFun
La Geometría Fractal está presente en los recientes avances de campos de estudio tan diferentes entre sí como la medicina, biología, astronomía, geografía, arquitectura y tecnología. Queda patente que, además de ofrecer contenidos extracurriculares, la Geometría Fractal permite establecer conexiones didácticas entre muy diferentes áreas de estudio; creando escenarios transversales, ideales para que nuestros alumnos sientan la libertad de tomar el camino que deseen durante su proceso de aprendizaje. A esto hay que sumar la ventaja de que, tomen la dirección que tomen, llevarán consigo una buena base matemática que, con toda seguridad, les resultará de utilidad en cualquier otra área.
Con esa premisa nació el Proyecto FractalFun*, ideado para dar a conocer de un modo sencillo e intuitivo el concepto de "Geometría Fractal" mediante el uso de su propio software, FFExplorer, que se encuentra en constante evolución desde 2010 para facilitar el estudio y la experimentación con fractales.

En la actualidad, diferentes programas de enriquecimiento educativo se apoyan en la experiencia de FractalFun con el objetivo de desarrollar en sus alumnos nuevas habilidades y conocimientos que les permitan reconocer y aplicar ideas geométricas más allá de las propias matemáticas, como podría ser en el arte, en la naturaleza o en la arquitectura. De esa manera, sus alumnos son más eficaces a la hora de encontrar soluciones creativas para afrontar los problemas que se les presentan en su día a día.

Como segundo objetivo, este proyecto se enfoca en que los alumnos desarrollen conocimientos que les doten de destrezas superiores a las que puedan recurrir el día de mañana para afrontar posibles situaciones y problemas que se les presenten dentro de sus distintas áreas de estudio o de trabajo.
Los siguientes vídeos muestran algunas de las actividades realizadas por los alumnos del Área de Geometría Fractal:
Para más información sobre el proyecto, por favor dirígete a 
O quizás ya tengas un plan y tan sólo necesites un "Software explorador de Fractales"
(*) Este proyecto y su software se llamaron "Fractfinder" y "Explorador FF" hasta 2018.
Explorador de Fractales
FFExplorer es un software para Windows, portable y gratuito, que ha sido creado de acuerdo con la filosofía del “Proyecto FractalFun” para la experimentación con fractales de forma sencilla e intuitiva. Desde que dio el salto a Internet en 2010 no ha parado de evolucionar, adaptándose con nuevos algoritmos y funcionalidades a las necesidades específicas de los alumnos e instituciones que hacen uso de él.
¿Qué puedes esperar de FFExplorer?
Si vas a explorar fractales por primera vez, el software te ofrecerá la posibilidad de olvidarte de números y fórmulas. Podrás dedicarte plenamente a descubrir y disfrutar con tan sólo interactuar mediante el uso del ratón diréctamente sobre las imágenes fractales.
Si, por el contrario, este no es tu primer contacto con los fractales, el software te ofrecerá la posibilidad de darle un uso más avanzado. Podrás modificar los parámetros y comportamientos de los algoritmos para crear infinidad de variaciones de los fractales originales, así como crear tus propios algoritmos fractales desde cero.
FFExplorer incluye una gran variedad de algoritmos fractales, de coloración y de iluminación; pero también podrás encontrar en él multitud de herramientas que de una forma u otra se relacionan con los fractales, o interactúan con ellos:
- Compilador de fórmulas para la creación de nuevos algoritmos.
- Renderizador de Descriptores Lagrangianos Discretos. nuevo
- Proyector estereográfico de fractales sobre Esferas de Riemann.
- Generador de fractales mediante Agregados Limitados por Difusión.
- Generador de patrones caleidoscópicos a partir de fractales.
- Generador de mapas de Julia a partir de fractales de Mandelbrot.
- Generador de ruido celular basado en Diagramas de Voronoi.
- Diseñador de trampas orbitales complejas basado en “Superfórmula”.
- Diseñador de diagramas de multiplicación.
- Diseñador de árboles de Pitágoras fractales.
- Diseñador de copos de nieve fractales.
- Diseñador de fractales de Sierpiński.
- Diseñador de fractales Lineales.
- Diagramas de bifurcación.
- Atractores extraños. nuevo
- Diseñador de laberintos aleatorios. nuevo
- Autómatas celulares basados en reglas o en el Juego de la Vida de Conway.
- Sistemas complejos basados en el Modelo de Boids de Craig Reynolds.
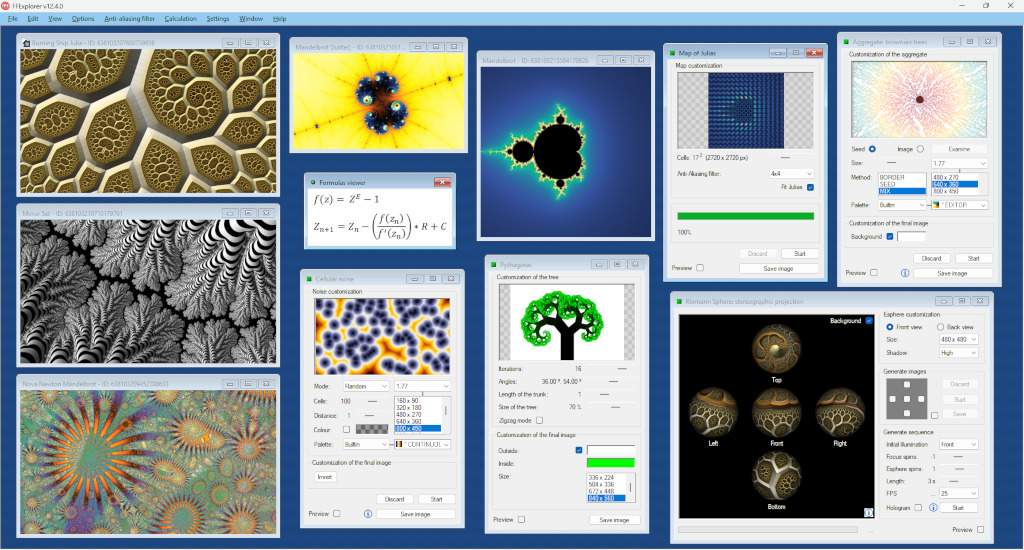
Como muchas de las herramientas del software interactúan entre sí, este ha sido diseñado con una interfaz que funciona a modo de escritorio, para poder colocarlas libremente donde se desee y así poder trabajar con ellas cómodamente.
« FFExplorer es sencillo de utilizar, versátil y adaptable. Con él se obtienen imágenes fractales muy variadas que se pueden utilizar para diversos fines, entre ellos diseñar sorprendentes animaciones, o crear Arte Fractal de excelente calidad. Una vez generada la imagen se puede optar por utilizar un editor gráfico con el que retocarla, pero yo personalmente prefiero buscar el aspecto final deseado para la imagen tan sólo explorando el fractal, y utilizarla directamente sin retocar, de manera que conserve y muestre toda su esencia matemática intacta. No obstante, además de ser un software que te permite un gran nivel de control para generar preciosas imágenes con el aspecto que desees, FFExplorer no deja de hacer honor su nombre, ya que te permite explorar fractales, y eso es una experiencia asombrosa. Yo cuando empiezo no puedo parar... »
ElenSegu, experta en diseño y Arte Fractal
Aquí puedes descargar la última versión de "FFExplorer"
Y aquí puedes echar un vistazo a "FFExplorer en cifras"
Arte fractal
El concepto de arte admite muchas interpretaciones, lo que hace muy difícil su definición, pero se podría decir que las más extendidas hablan de su capacidad estética y comunicativa para transmitir ideas y sentimientos, es decir, todo lo ligado a nuestra parte más emocional...
Entonces parece una contradicción cuando se habla de crear arte con matemáticas, una materia que nos recuerda palabras como "precisión", "cálculo", "análisis"... conceptos fríos asociadas al pensamiento racional y aparentemente de naturaleza incompatible con el arte.
Sin embargo todo ello cambió gracias a la Geometría Fractal: un fractal es la representación gráfica del comportamiento de una fórmula matemática, con la que su autor ha experimentado hasta conseguir el aspecto deseado. Esa experimentación consiste en el ajuste numérico de determinados parámetros, en la introducción de pequeñas transformaciones y en un buen tratamiento del color. Con todo ello se consigue un entorno gráfico explorable, en el que además de las dos dimensiones del plano existe una tercera dimensión (no convencional) que solo es accesible haciendo zoom. En este mundo virtual, su creador puede moverse libremente y buscar la zona y el encuadre deseados para finalizar su obra.

El arte fractal tiene propiedades muy exclusivas:
Complejidad. El complejo funcionamiento de las fórmulas, en apariencia sencillas, es responsable de la gran explosión de formas y colores que dotan a las imágenes fractales de un gran nivel de detalle perceptible a diferentes escalas. Esto hace que una pieza de arte fractal de grandes dimensiones muestre detalles muy diferentes dependiendo de la distancia desde donde se observe, haciéndose así más notable su característica auto-semejanza y el efecto de la tercera dimensión.
Perfección. El aspecto de una imagen fractal está perfectamente definido por la configuración del algoritmo que la dibuja, esto quiere decir que la fórmula y los valores numéricos introducidos en ella son una seña de identidad única y exclusiva de la imagen. Conocer estos datos permite volver a dibujarla cuantas veces se desee, por ejemplo, para seguir trabajando sobre ella, o para generar una copia de la original a mayor resolución sin pérdida de calidad (sino todo lo contrario, un mayor tamaño aumenta su definición).
Exclusividad. La fórmula que dibuja un fractal es muy sensible a los valores de sus parámetros, de modo que una ligera variación en alguno de ellos producirá una imagen completamente diferente. Gracias a ello, resulta prácticamente imposible volver a dibujar una imagen fractal si no se conoce la fórmula y los valores exactos que se emplearon originalmente, lo que permite demostrar quién es el autor de la imagen ya que evita que alguien diferente pueda realizar copias exactas de la obra.
Si te ha parecido interesante, quizás quieras saber qué es el "Fractivismo"O puedes visitar las Redes sociales de FractalFun:








 DeviantArt:
DeviantArt:  DeviantArt:
DeviantArt:  Facebook:
Facebook:  ¿Qué es un fractal?
¿Qué es un fractal? Sistema Planetario de Shaula:La esfera de Riemann
Sistema Planetario de Shaula:La esfera de Riemann Trabajo de investigación:Cardioides, epiciclos y diagramas
Trabajo de investigación:Cardioides, epiciclos y diagramas Dimensión Fractal - Colaboración entre Croacia y España -
Dimensión Fractal - Colaboración entre Croacia y España -